EXERGY
- A USEFUL CONCEPT WITHIN RESOURCE ACCOUNTING

Göran Wall
Report no. 77-42, Institute of Theoretical Physics, Chalmers University of Technology and University of Göteborg, S-412 96 Göteborg, Sweden

Preface

Anxiety concerning the problems of energy and resources has led to a rapid increase in the interest in describing and understanding the conversion processes of energy and other resources in society. To be able to understand the procedure of these conversion processes it is important that useful concepts are available. I hope that this report will be a help in the development of such concepts.

This report has grown out of earlier collaboration with Björn Eriksson, Karl-Erik Eriksson and Kåre Olsson {1}. The manuscript has been read by Karl-Erik Eriksson and Are Kjeang. I hereby acknowledge my gratitude to them for many important comments and ideas. I am especially grateful to Margareta Ehinger for typing the report with great accuracy. I have received financial support for this work from the Secretariat of Futurological Studies and the Royal Swedish Academy of Sciences.

Of course, I would also be grateful for further comments on and criticism of the content in this report.

Göteborg, May 1977

Preface to internet version

Some figures has been updated with color graphics to add clarity. Otherwice, the text is the original text from 1977. Also, please note, that the address above is no longer valid.

Mölndal, January 1997

Contents

1. Introduction

2. Exergy

2.1. Energy, matter and quality
2.2. The concept of exergy
2.3. Examples of exergy carriers
2.4. Global and local standard environments

3. Exergy and resource accounting

3.1. Exergy, a concept in natural sciences
3.2. Exergy of natural resources
3.3. World trade and exergy flows
3.4. Difference between energy and exergy descriptions
3.5. Exergy and other resource measures
3.6. Flows, deposits and funds
3.7. Exergy conversion in Swedish society
3.8. Concepts of efficiency
3.9. Exergy analysis

4. Exergy and information

5. Concluding remarks

Appendix A: Derivation of the exergy concept

Appendix B: Exergy content of materials

Appendix C: Efficiency concepts at conversions of exergy

Appendix D: Exergy and information

Appendix E: Exergy and some idealized thermodynamical systems

References

1. Introduction

The purpose of this study is to discuss physical concepts for resource accounting and to suggest a number of basic concepts that could also be valuable in social and economic sciences.

The study has to be considered as a first attempt to summarize fundamental concepts and ideas for an expanded resource budgeting. In order to be able to further develop and establish the basic concepts presented here, however, these must be widely criticized and tested.

Particularly within energy planning, there is now much confusion as to concepts and appropriate delimitations. We often try to solve this concept confusion by introducing new energy units, such as Watt-hours electrical energy (Whel), tons oil equivalent (toe) etc {2, 3, 4}. Instead, problems arise when comparing energy measured with different units. Furthermore, there is the problem of the different definitions of these units in different countries, depending on how the energy form is produced. For energy conversion processes, completely misleading efficiency concepts are often defined, that reflect reality in a false way {5, 6}. The energy and efficiency concepts used today cannot be applied in an expanded resource budgeting without further notice. The main reason for this is that these concepts lack a fundamental connection to the physical environment. At certain conversions, the environment is of great importance such as, e.g., at the space heating process.

The relationship between the physical resource base and the social and economic structure {7, 8} is a condition often neglected by historians, social scientists and economists. Scientists who have described the physical resource base have, on the other hand, often been little interested in social and economic structures in society.

There are, however, exceptions. There are economists who have tried to take physical factors into consideration as well as economic factors {9, 10, 11}. There are scientists who have taken an interest in catastrophes and threats caused by man's actions and their squandering of natural resources {12}. Ecological aspects have been of great interest for speculations in this field during the last few years {13,14}. Within the Secretariat of Futurological Studies, two very interesting projects are being carried out in this connection, Energy and Society and Resources and Raw Materials . From these projects progress reports are continuously published {15} that are of great importance for the comprehension of the energy and material conversion in society {16}. An increased comprehension of the energy and material conversion processes is necessary when planning for the future. Interest in these processes has increased recently in society. The theme of the yearbook of the Swedish Natural Science Research Council 1976/77 is "Natural Resource Cycles" {17}. In order to be able to answer the question about which technology we should choose and how this technology is to be used, knowledge of nature and its cycles is needed. This is because the functions of our own society are integrated in the conversion of energy and matter in nature.

The fundamental concepts that I principally discuss in this study are exergy {18 - 21} and efficiency {22}. The exergy concept has recently appeared more and more often in technical literature {22 - 25}. Exergy represents the useful part of energy for a system in its environment, i.e. the maximum quantity of work that the system can execute in its environment. The exergy concept derives from the entropy concept or rather the negentropy concept {26}, that is more useful in this connection.

The thermodynamic presentation of the exergy concept is given in Sections 2.1 and 2.2. (The derivation of the relevant thermodynamic relations is given in Appendix A.) In Section 2.3, energy and matter are treated as carriers of exergy. In Section 2.4, I discuss the exergy dependence on the environment and the necessity of defining useful standard environments.

Schrödinger {26} says in his book What is life? that "we feed on negentropy". He might as well have said "we feed on exergy". Exergy is the fuel for all systems with the ability to maintain themselves, such as the biosphere, an ecosystem, a species, or a living organism. Exergy studies should therefore be useful within those sciences which deal with such systems. In Sections 3.1, 3.2 and 3.3, I give a very brief account of the conversion of exergy on earth. The exergy reaches the earth by means of sunlight, which is then converted, and thus maintains the living conditions for almost all living things on the earth's surface. The sociosphere constitutes the systems of the earth that are created by man. In this sphere world trade is an important exergy flow. There is a short comment on world trade in Section 3.3.

By starting from the energy conversion in a condensing power plant, we can clearly see differences between points of view in exergy and energy studies. These points of view can then be futhered to the energy conversion of a society. This was accounted for in Section 3.4. A first attempt to extend the exergy concept to also describe conversions of matter is made in Section 3.5 and in Appendix 2. To be able to unite the exergy conversion of human society with the global exergy conversion, I account for the exergy flow in Section 3.6. The human society today is dependent on exergy flows from finite deposits of exergy in minerals, such as ores and fossil fuels, but first of all on renewable exergy flows from funds, such as forests and fields, which convert solar energy. Human individuals, groups and societies are constantly dependent on exergy flows to meet their needs. We usually talk about energy resources, material resources such as ores, food and other biological matter, and the environment's ability to purify itself. All these phenomena, however, are examples of exergy flows and can, at least in principle, be quantified in a unified way. This is illustrated in Fig. 3.9, Page 31, where the exergy conversion in Swedish society is presented. From this physical description of a society, we can then start discussing efficiency concepts and comparing different definitions of efficiency. In Section 3.8, I compare energy efficiency and exergy efficiency as concepts of efficiency. The natural consequence of this will then be the question of how effective the total exergy conversion is in society. The aid for such an analysis is described in Section 3.9, Exergy analysis.

In Chapter 4, I discuss the relation between the concept of information, from information theory, and the exergy concept. There is a fundamental relation between these concepts, which are both measurements of order, structure, and contrast.

Chapter 5 is simply a brief concluding remark.

Further, there are five appendixes to the report, which give a more formal description and extension of the concepts presented in the text.

2. Exergy

2.1. Energy, matter and quality

Energy and matter cannot be created or destroyed nor produced or consumed. This is a fundamental law of nature. There are no sources or sinks for energy and matter. Energy and matter can only be converted into different forms. This occurs by the consumption of quality. Locally, the quality can be improved, but this can only occur at the expense of a greater deterioration of the quality elsewhere. On the whole it is a question of continuous deterioration in quality. This is also a fundamental law of nature.

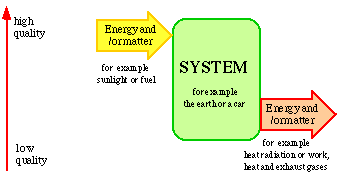
The situation is illustrated in Fig. 2.1. Energy and/or matter flow through a system. This must be well defined as to time and space. The motive force of the flow of energy and/or matter through the system is the quality. The quality of the energy and/or matter constantly deteriorates in the flow passing through the system. This is a condition if the flow is to have a definite direction and be defined as to time.

Figure 2.1. The flow of energy and/or matter through a system

When energy and matter flow through a system, a very small part of this is often stored in the actual system. There is usually a balance between inlets and outlets of energy and matter.

Energy and matter only serve as carriers of quality, and it is the quality that is consumed during the conversion of energy and matter. According to this way of looking upon flows of energy and matter it is wrong to talk about the fact that energy and matter are produced or consumed. It is only quality that can be produced or consumed. If an old car stands in the open air getting rusty the material deteriorates in quality but the matter still exists. It will combine with the environment in new chemical combinations, i.e. new materials. From social economic viewpoint, we can say that the car and its material decrease in value and, as time passes, become of no value.

Flows of energy and matter can be regarded as two different phenomena which transport quality. The nonphysical distinction between these is often unclear and approximate. A certain flow can often be regarded both as a flow of energy and as a flow of matter. More about this in Section 2.3 below. The abstract phenomenon of quality is information, which is discussed in Chapter 4.

Instead of saying that the quality decreases, we can say that the lack of quality increases, or that the entropy or disorder increases. It is stated in the second law of thermodynamics that conversions of energy and matter must always take place from a state of low thermodynamic probability to a state of high thermodynamic probability. The energy and matter tend to be distributed over a steadily increasing number of possible states. The quality decreases, and the contrast in a system or a flow is more and more wiped out. An example of this is a warm and a cold flow where the quality and the contrast are determined by the differences in temperature between the flows, which are then mingled to a tepid flow. A tepid flow has no contrast and has, therefore, lower quality than the original flows. This is expressed quantitatively in statistical mechanics as an increase of the entropy for the entire system. The entire system consists of all inflows and outflows as well as all the conversion systems between them. The entropy, represented by an S, can be written as a sum:

where k = Boltzmann's constant, = the number of permitted states for the total system, and Pi is the probability for all permitted states which is standardized so that the sum will be equal to one, i.e.:

The probability for a state can be directly compared to the knowledge of the total system. If we know for certain that the total system is in a certain state, the probability for this state is equal to one. The probability for other states must thus be equal to zero according to Eq. (2). The knowledge of the entire system is thus complete and the entropy for the total system is equal to zero (S = 0). Order is complete. On the other hand suppose we do not know anything about the total system. All permitted states must then be equally probable. The number of permitted states is . The probability of each state is thus, according to Eq. (2),equal to one divided by this number, i.e. 1/. The entropy for the total system becomes S = k ln . This is the maximum value of the entropy. Disorder is complete.

A conversion of energy and matter which takes place at a finite rate inevitably leads to an entropy production. The entropy production increases with the rate of the conversion. E.g. if we let the conversion take place at a low rate the entropy production becomes less than if the same conversion takes place at a high rate. A conversion which can be reversed is called reversible. Such a conversion is infinitely slow but does not involve a loss, i.e. there is no net production of entropy within the system during the conversion itself. There can, of course, be local changes of the entropy within the system, but on the whole there is no entropy production i.e. no losses of quality. However, a reversible conversion is never completed because of this, and therefore lacks a definite direction of conversion. Reversible conversions only exist theoretically. Real conversions of energy and matter are never reversible. They are always irreversible, which means that they always occur with a loss. Contrary to reversible conversions, irreversible conversions have a definite direction. Losses at real energy and matter conversions are therefore inevitable, and they are also to some extent necessary. Each desired conversion must involve losses, but the losses can be kept down. I have already mentioned a way of keeping down the losses, namely by keeping down the rate of the conversion. There are many other ways, for example choosing the conversion that involves the smallest losses. I will describe this later in connection with energy conversion processes.

The entropy concept is a measurement of the lack of quality. Due to this, the entropy concept gets a negative meaning. We can give a definition of the opposite of entropy, negative entropy or negentropy (-S ). Negentropy thus becomes a direct measure of quality {26} and has a positive meaning. Negentropy is consumed when quality is consumed or lost.

2.2. The concept of exergy

How shall we measure the quality of a system or a flow of energy and matter? In the technical literature on energy the value of being able to estimate the useful part of the energy, that part that can perform mechanical work, has long been stated {27-30}. In 1953 Z. Rant suggested that the term exergy (in German Exergie) {18} should be used to denote "technical working capacity" (in German technische Arbeitsfähigkeit). A complete definition was given by H. D. Baehr {19}:

Exergy is that part of energy that is convertible into all other forms of energy. (Die Exergie ist der unbeschränkt, d.h. in jede andere Energieform umwandelbare Teil der Energie).

The exergy of a system in a certain environment is the amount of mechanical work that can be maximally extracted from the system in this environment. Some examples of systems are a solid, a body of gas, e.g. the air in a heated house in a wintry environment, or a certain quantity of fuel, e.g. the petrol in the petrol tank of a car. The concept of mechanical work below is to be regarded only as an example of a totally ordered energy form, i.e. with the entropy equal to zero. It is only the useful or ordered part of the energy that can be converted into all other energy forms.

Baehr's definition is obviously very general, and can be extended to concern not only energy but also matter. This extension will later be found to be completely justified. An ordinary battery can be used as an example of the conversion of different forms of matter. The matter is converted from one form to another through chemical reaction, and exergy can be derived in the form of an electric current.

Thus, the matter has a greater exergy content in a charged battery than in a discharged battery. The exergy content today is principally used at the optimizing of the steam process within the power industry.

R. B. Evans {20} has shown that exergy (which he calls "essergy") in itself incorporates other thermodynamic concepts such as Gibbs' free energy, Helmholtz' free energy, enthalpy (a simplified derivation of this is given at the end of Appendix A), and "availability" introduced by Keenan {30, 31}. Another quite adequate name, "available work" was used by a working team within "the American Physical Society (APS)" in the summer of 1974 {22}.

Exergy is a measurement of how far a certain system deviates from a state of equilibrium with its environment. In Appendix A the exergy E for a system in an environment is written as

where T ₀ is the temperature of the environment, is the entropy of the total system, i.e. the system plus the environment when the system is in equilibrium with the environment ("eq" stands for equilibrium), and is the entropy of the total system at a certain appropriate deviation from equilibrium. In Appendix A, it is also stated that this concept of exergy is a result of the above definition of exergy. The concept (3) is thus equivalent to Baehr's definition. Exergy is a general concept of quality, i.e. the physical value of a system in the form of how large a quantity of purely mechanical work can be extracted from the system in its interaction with the environment.

By using thermodynamic relations, other concepts of exergy can be derived (see Appendix A).

where U , V , S and ni denote extensive parameters (i.e. quantities that increase with the size of the system) of the system (internal energy, volume, entropy and the number of moles of different chemical elements) and p ₀, T ₀, i ₀ denote intensive parameters (i.e. quantities which are independent of the size of the system) of the environment (pressure, temperature and the chemical potential of the component "i " in its standard state, i.e. in equilibrium with the environment).

Thus, the exergy of a system shows how far the system deviates from the environment. We can see this clearer from the definition (5) below. When the temperature, pressure and chemical potential are the same for the system and for the environment, the exergy of the system is equal to zero. We can also see that the exergy of the system increases when the contrast, the deviation from the environment, increases.

The following formula is very useful for determining the exergy {22},

where on the right side easily determined quantities appear ("eq" denotes equilibrium with the environment). The derivation is given in Appendix A. It is therefore an easy task to determine the exergy content of a given system in a given environment.

The exergy content in a material can be determined by the formula (see Appendix B):

where is the chemical potential for the matter "i " in its reference state (a state to which all values of the chemical potential for a certain matter are related) and ci is the concentration of the component "i ". This way of expressing the exergy makes it possible to determine the exergy content in each type of material theoretically. The exergy content in a given quantity of a certain material can be considered as the quantity of exergy needed to produce this material from the given standard environment by reversible processes.

2.3. Examples of exergy carriers

In Section 2.1, I described how a flow of energy and matter is driven forward by the fact that the flow all the time continuously loses in quality. The quality was also described as the absence of disorder, i.e. of entropy. In Section 2.2, the exergy concept was defined. In this section, I will now link together the two sections by considering energy and material flows exclusively as carriers of exergy, so-called exergy carriers .

The quality of an energy form can be expressed as the quantity of negentropy per unit of energy for the energy form in question. The purest energy forms are mechanical and electrical energy, for which the negentropy is zero (-S = 0). Energy in the form of heat has a lower quality. The quality decreases with the temperature (provided that the temperature is higher than the environment). Baehr's definition makes it clear that the exergy concept incorporates both the quantitative and qualitative properties of energy.

In Table 2.1 different forms of energy are listed according to their quality, decreasing from "extra superior" to "valueless" {32}. The quality of the energy is indicated by an index giving the approximate exergy content as a percentage of the energy content. The quality index ranges from 100 for potential energy, kinetic energy and electricity (which are pure exergy and thus can be totally transformed into all other forms of energy) to 0 for the exergy-lacking heat radiation from the earth. The quality index of heat energy varies considerably from 60 for hot steam to zero for heat radiation from the earth.

Table 2.1. The quality of different forms of energy.

	Form of energy	Quality index (Percentage of exergy)
Extra superior	Potential energy1 Kinetic energy2 Electrical energy	100 100 100
Superior	Chemical energy3 Nuclear energy4 Sunlight Hot steam District heating	About 100 (corrected) 95 (corrected) 93 (corrected) 60 30
Inferior	Waste heat	5
Valueless	Heat radiation from the earth	0

1. e.g. highly situated water resources

2. e.g. waterfalls

3. e.g. oil, coal, gas or peat

4. e.g. the energy in nuclear fuel

However, not only energy-containing systems carry exergy. If a system is deprived of energy (and thus deviates in this way from the environment) it carries exergy. An ice-block in an environment at room temperature is an example of such a system. (Due to this, the ice represents a negative energy content). When the ice melts, it takes energy from the surrounding air, but we can use the difference in temperature between the ice and the air to run a heat engine and thus extract useful work. This makes the ice a source of exergy. In an analogous manner, an empty container, i.e. a vacuum, surroun- ded by air and at normal pressure, contains exergy and can be utilized to extract work.

Analogous to the quality of energy, the quality of a certain material can be expressed as the amount of exergy (per unit) for the material in question. The purest form of matter is that consisting of only completely known elements, for which the entropy is almost zero. Diluted and mixed matters have a higher entropy, and therefore have a lower quality. The quality decreases with a greater extent of dilution or mixture. A concentrated mineral deposit has a high exergy content. By mining the mineral deposit and distributing it in the environment, the exergy content decreases. In Table 2.2 different forms of material are listed after decreasing quality. It is difficult to make a classification such as the one in Table 2.1. In any case, there is a clear difference between the upper part of the table, which can be considered as "extra superior" and "superior", and the lower part, which can be considered as "inferior" or "valueless".

The quality of the material form is expressed by an index giving the approximate exergy content i.e., the amount of "elements in an ordered form", as a percentage of the amount of the material. The definition of the quality index is here analogous to the defintion of the quality index for the energy forms in Table 2.1, where the quality index was the amount of "extra superior energy" as a percentage of the amount of energy in question. The exergy for a material is thus the amount of "elements in an ordered form" that can be extracted from a system in its environment. Thus, from a given amount of material, only the part given by the exergy content can be refined into a pure form, provided that no consumption of external exergy occurs. When estimating the exergy content for the material in question, Eq. (7) has been used. As the exergy does not differentiate between "extra superior energy" and "matter in an ordered form", there is here a clear connection between energy and matter. (Einstein's relation between energy and matter, E =mc², the energy is equal to the mass times the speed of light squared, is another more fundamental relation.) Accordingly, we can exchange extra superior energy for the same amount of exergy in the form of matter in an ordered form. This is what we do when enriching and refining a mineral deposit into pure material. We exchange, so to say, exergy in the form of energy for exergy in the form of matter.

Table 2.2. The qualities of different materials i.e. forms of matter.

1. e.g. carbon in the form of diamond

2. e.g. iron, gold or lead

3. e.g. steel, alloys or plastics

4. e.g. bog iron (limonite) or sea nodules

5. e.g. bauxite

From Table 2.2, we see that a qualitative index ranges from 100 for absolutely pure and atomically well-ordered materials such as diamonds, to almost 0 for materials evenly distributed in the soil or completely dissolved in seawater. The value of a qualitative index depends on in which environment the exergy is estimated. In Table 2.2, the estimate of the exergy content of the different materials was made with the earth's average combination of material as environment. This means that those materials which are common on earth are of a low exergy value. A comparison with energy forms in Table 2.1 can be made, where heat radiation from the earth is considered as worthless.

Exergy-rich systems, such as chemically concentrated materials, can, in practice, be utilized in chemical-electrical cells of concentration type. At a river mouth, the exergy-rich fresh water literally flows into the sea. If the fresh water is made to mix with the saltwater in a controlled process, work (exergy) could be extracted. An estimate proves that the outlet of the river "Göta Älv" into Kattegatt is equivalent to a waterfall at a height of more than 100 metres. This might become an important energy source for the future. (The exergy content of fresh water is also illustrated by the fact that enormous energy quantities are needed to desalt seawater.) The exergy content in concentrated deposits of minerals will be further dealt with in connection with our discussion on resource accounting.

2.4. Global and local standard environments

As the exergy of a system is determined according to its environment, it is important to agree on suitable reference environments to be used. A global standard environment can be defined in terms of a standard atmosphere with a standard sea at sea level (for gravitational exergy, such as potential energy and tidal energy, the average sea level is a general standard), where the standard states are related to average geophysical conditions. For exergy analyses of traded goods, and for the use of exergy in the earth sciences, such a standard state is necessary.

Temperature conditions differ widely between different parts of the earth, as does the air pressure. Similarly, the chemical potentials of the water in lakes and rivers differ substantially from those of the sea. The structure of the ground and bed-rock varies much over the earth's surface as well as on the bottom of the sea. Thus it is necessary to introduce local standards of exergy also. The most obvious advantage of such local standards is in describing the use of energy (consumption of exergy) in space heating. By adapting the building technique to the prevailing climate, the consumption of energy for heating can be kept down. The relation between global and locally defined exergies of a system is given in Appendix A.

To what extent local standards should be averaged through time, or vary with seasonal or daily variations, is a question that needs to be studied. For the description of space heating seasonal variations are clearly essential. When local standards are used, the local exergy content of a system will consequently vary with the location. This variation may be related to the economic value of the system. A flow of energy and matter can e.g. change its exergy content when passing between different environments. The contrasts between e.g. an ice-block and its environment in Greenland or in tropical Africa are quite different. This variation may be related to the economic value of the system. An ice-block is worthless on Greenland, but it could be valuable in tropical Africa.

3. Exergy and resource accounting

3.1. Exergy, a concept in natural sciences

On the surface of the earth, at many different levels of size and time scale, systems operate involving many kinds of matter in a complex pattern. Energy and matter permanently flow through different systems on the earth's surface. Within many sciences, e.g. hydrology, climatology, oceanography and ecology, we are trying to describe and understand parts of these systems and flows. It may be a supernatural task to try to understand how all these systems and flows of energy and matter cooperate. We can easily split up all the systems of the earth's surface into 5 different spheres, see Fig. 3.1.

Fig. 3.1. Five spheres in mutual interaction.

The atmosphere is the air that surrounds the earth, principally consisting of nitrogen (about 80%) and oxygen (about 20%) plus a few percentages of other gases such as carbon dioxide, water vapour and ozone. The atmosphere is retained around the earth by gravitation, that is determined by the mass of the earth. Water is the only matter on earth that can simultaneously exist in the three states of aggregation, solid, fluid and gas, because we can have ice, water and water vapour at the same temperature on earth. Furthermore, water is an enormous heat reservoir, thereby balancing local temperature variations on earth. The lithosphere is the solid bed-rock with all its minerals and salts. Through erosion, these matters are dissolved and are then important nutritive salts in the water. The biosphere consists of all living organisms on earth, and the sociosphere consists of all the systems ruled by man. Plants and animals consequently belong to the biosphere, and buildings and machines belong to the sociosphere. Only so-called primitive people and their tools belong to the biosphere. All these spheres influence each other. An example of this is the oxygen of the air, sediment, fossil energy deposits, and the DDT content in the biosphere. Figure 3.1 illustrates this influence as lines between the spheres. The communication between them is carried on by means of exergy. Exergy is consumed in the constant flows of energy and matter that go on within and inbetween these spheres. The driving source for the whole system is exergy that is pumped into it from outside. This process is illustrated by a schematic diagram in Fig. 3.2.

Exergy from the contrast between the sun and space drives flows of energy and matter through the spheres on the earth's surface. We see in Fig. 3.2 that there is a balance between the inflow and the outflow of energy. The average temperature on the earth's surface is determined by, among other things, the amount of energy that radiates towards the earth. Matter is transported via countless cycles through systems on earth. The circulation periods for these cycles of matter can vary from splits of seconds to billions of years. Examples of parts of such cycles can be nerve impulses in a cell and mining in a human society.

Figure 3.2. Flows of energy and matter on earth are driven by the contrast between the sun and space.

When exergy reaches the earth, it is gradually destroyed, but on the way it manages to drive, among other things, the water/wind system, and life on earth. Merely the water circulation in the hydrosphere takes about 7000 times the energy which is converted in the sociosphere by man {33}. Complex structures, rich in energy and capable of reproduction, are formed by photosynthesis in the biosphere. The green plants pick up exergy from sunlight by photosynthesis, and convert it into chemical exergy in materials, which then pass through different food-chains. At every link, exergy is consumed. The last link represents micro organisms, which decompose the materials. The exergy that cannot be utilized by these organisms forms peat instead, that gradually becomes stores of oil or coal. Stores in the form of living and dead organic matter on earth thus represent different forms of stored exergy.

The energy balance of the earth and the related exergy consumption can be illustrated by means of Fig. 3.3:

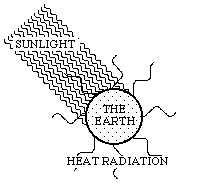
Figure 3.3. Short-wave sunlight inwards, and long-wave heat radiation outwards.

Energy-rich sunlight reaches the earth. A lot of it is reflected directly, and therefore it does not join in the conversion processes on the earth's surface. In Fig. 3.3, this part of the process was omitted and the inflowing sunlight is thus the net flow of sunlight reaching the earth. The energy of this flow is converted on earth, and thereafter it leaves the earth as heat radiation. The exergy of the sunlight is, however, consumed on earth. Figure 3.3 illustrates this process as a change of the wave-length between the inflowing sunlight and the outgoing heat radiation. The inflowing solar radiation is relatively short-wave and therefore has a high quality. The outflowing heat radiation is, however, long-wave and consequently of low quality. The whole of the earth can thus be seen as an immense machine picking up exergy from the sun. Due to this, all flows of energy and matter are carried forward through systems on the earth's surface, and life can be created and maintained. The motive force is always the difference in quality between visible sunlight and outgoing invisible heat radiation.

In order to steer a process, e.g. a metabolic process in a living organism, along a definite direction, a thermodynamic irreversibility is needed. An increase in security can be obtained through an increase in irreversibility. This is obtained at the cost of an increased energy dissipation, i.e. an increased exergy consumption . The steering of a process in a definite direction must, therefore, use exergy. Processes of life and thermodynamics have been studied by Glansdorff and Prigogine {34} and Eigen {35}.

In H.T. Odum's diagramatic description of ecological systems {13}, energy plays a fundamental role, which would probably be better played by exergy.

Metabolic processes in living organisms and eco-systems have analogous counterparts in human societies. Experience in describing natural systems ought to be of great help in describing human societies {36}.

3.2. Exergy of natural resources

By using the exergy concept, we can describe various types of resources used in a society in terms of a common physical unit.

The so-called energy resources have exergy contents that are very close to the energy values often given. Either they are of a mechanical form (hydro-power, wind power) which, by definition, is 100 percent useful work, or they are of a high-grade chemical form, for which the commonly accounted enthalpy is rather close to the exergy value {30}. In conversion through heat, we lose a large fraction of the exergy, see Section 3.4. One way to overcome this difficulty is to develop fuel cells that can convert chemical exergy directly into electricity.

In ascribing a definite exergy value to nuclear fuels, several difficulties arise, such as neutrino radiation and the lack of a well-defined final state.

But there are also resources other than the energy resources that have exergy. A concentrated metal ore contrasts against the normal chemical composition of the background. The exergy due to this contrast is retained when the ore is mined. When the ore is enriched and reduced to metal, the exergy of the material is increased, the added exergy coming from fuels and reducing agents used in the process, see Appendix B. The exergy is not destroyed until the metal products made from the metal piece in question are rusting or being dispersed {38}.

Minerals that are very common in the earth's crust or in seawater - such as sand, salt or water - have little exergy, and they are also generally less of a resource problem. In an arid zone, however, water can be a precious resource, but in that particular local reference environment it also carries a lot of exergy.

Biological materials have exergy in two forms - chemical and structural of which the chemical exergy dominates quantitatively. When a fuel is burnt, the chemical energy is transformed into heat, whereby, depending upon the flame temperature, more or less of the exergy is destroyed.

The structural exergy lies in the low entropy ("improbable") shapes that living matter takes. We utilize these when using wood as a construction material, or wool as a fibre. When using biological matter as food, we use both the chemical exergy (as fuel for the metabolism) and the exergy of the micro-structure of amino acids and vitamins (for building the body and substituting worn-out cells). After a biological material has been used as structural material, almost all of the exergy is left and can be exploited as a chemical exergy source, e.g. fuel.

The interesting point of the above discussion is that all kinds of natural resources evidently can be accounted for in the common entity, exergy, which is an expression for both the ability to perform work and the structure of information in the system. What it measures is the alternative physical work that would be required if all inputs to the process instead - with total reversibility - were taken from the standard reference environment.

3.3. World trade and exergy flows

International trade can be seen as a resource flow, measurable in terms of exergy. Exergy analysis might throw some new light on international trade by providing information which is complementary to the monetary data mostly used.

An interesting point is that the exergy requirement for the production of a given product differs from place to place, depending on the differing reference environments. This is one of the reasons for trade. An analysis of this would help in finding to what extent trade is caused by differences in natural resources, in local reference environments or in the structure of production systems.

3.4. Difference between energy and exergy descriptions

The exergy concept is today primarily used within the steam power engineering, where energy forms of different qualities are dealt with. Many of the energy forms from Table 2.1 are represented. It is shown here that for hot steam, district heating and waste heat the quality index, i.e. the exergy in relation to the energy content, becomes lower and lower. This must be taken into account by those engineers who work with these different energy forms.

Let us make a closer study of how a power plant works. The upper part of Fig. 3.4 below is an outline of a power plant, in this case a condensing power plant, where the combustion of oil or coal takes place. It could also illustrate a nuclear power plant, where uranium is used instead for creating heat. The heat produced is used to boil water under high pressure in a large boiler, in principle a large pressure-cooker (steam production unit). The steam is lead to a turbine, where the steam pressure is converted into rotation of the turbine shaft. At the other end of the shaft, an electric generator is located, producing electricity. The electricity is then distributed to the consumer to be further converted.

When the steam passed through the turbine it transmitted exergy to the electric generator. After the turbine, the steam is chilled in a condenser to water, and brought back to the boiler. This cooling is necessary to optimize the power transmission in the turbine, since the turbine can work with maximal difference in pressure when the steam is condensed immediately after passing through it.

The chemical energy in oil and coal, or the nuclear energy in uranium, is thus transformed into electrical energy, but not without losses. The losses are great in an oil condensing power plant, no less than about 60%, and in a nuclear power plant they are no less than about 70%. Counting the total system, from the preparation of the energy raw material to the finishing treatment of the waste products, there are even greater losses. This is dealt with in exergy analysis in Section 3.9 below. Let us now see what happens to the losses in the power plant itself.

In the bottom part of Fig. 3.4 there are two diagrams of flows, so-called Sankey-diagrams. In the top diagram, the width of the flow is proportional to the energy content for the respective energy form, in the bottom diagram, the width is proportional to the exergy content. The first thing we notice is that the widths of the inflows and outflows in the two diagrams are almost equal. This is due to the fact that both the inflows and the outflows are very high quality energy forms. The quality indexes for the energy forms in question lie between 90% and 100%. For electrical energy the exergy content is as large as the energy content. The losses in the two diagrams are, however, quite different. At first we have losses in the furnace. The fuel is here converted into heat. In an oil or coal fueled power plant we get a flame temperature of about two thousand degrees (^oC). In a nuclear power plant the temperature is instead a few hundred degrees (^oC). The heat is then transmitted through heat exchangers to boiling water. The pressure is high, with the result that the water does not boil until it reaches a temperature of a few hundred degrees. Through the walls of the furnace, and through pipes, heat is transmitted to the environment, where it is lost. Heat is also led out with the exhaust gases, to keep the chimney of an oil and coal power plant free from condensed water. These furnace losses represent only a small percentage of the total energy conversion. We see, however, from the exergy diagram that something drastic happens. At this point, more than one third of the exergy is lost. We also see that it is lost in the process itself, i.e. only a very small part of the lost exergy leaves the power plant. The exergy flow just becomes narrower. Large quantities of entropy are created. This is due to the fact that the steam that leaves the boiler has a lower temperature and pressure than should be physically possible. The reason for this is limitations in the fatigue strength of the components included in the process, principally in the boiler and the turbine blades. In a nuclear power plant, more than half the exergy is lost at this stage of the process.

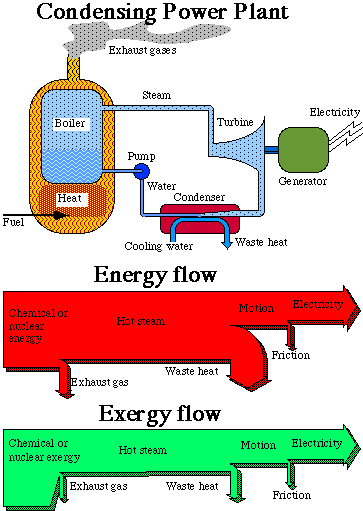
Fig. 3.4. The energy- and exergy flow through a condensing power plant.

The width of the flows of thermal energy and thermal exergy as hot steam in Fig. 3.4, show the greatest difference between energy and exergy flow. This is also a completely different view of how the losses in the process arise. In a diagram of energy flows, the losses are heaviest in the condenser. A great deal of the energy is lost in the condenser through waste heat in the cooling water. Waste heat is, however, heat at a very low temperature and therefore energy of a very low quality. This is clearly shown in the exergy diagram. The exergy content of the waste heat is just a small percentage of the energy content. To make it clearer we can picture the following process. Let us suppose that we convert the thermal energy in the waste heat into mechanical energy by an ideal process. From the waste heat, we would then only be able to convert that part of the energy content that corresponds to mechanical work, i.e. the exergy content. At such a conversion process the loss would be waste heat at the same temperature as the environment, i.e. with the exergy content equal to zero. It is by no means possible to attain more mechanical or electrical energy out of the thermal energy than what is determined by the thermal exergy.

When changing from mechanical energy to electrical energy, both with an exergy content of 100%, small losses arise through friction. These losses are on the whole equally small in both diagrams. Part of the friction losses consists of mechanical fatigue, i.e. wearing out of shafts and bearings.

The conclusion we can draw from the diagrams will thus be that in the diagrams of energy flows, the heaviest losses appear in the condenser but from the exergy flow, the heaviest losses seem to happen already at the combustion in the boiler. We also see from the diagram of exergy flows that these losses in the boiler cannot be extracted. Thus, the exergy is used in the process itself. It is a inevitable "internal loss", in the process and is dependent on the technical solutions available.

Let us now look at a larger system, the energy conversion in a whole society. For all of the governmental energy reports {2 - 4}, a lot of summaries of statistical data as to the extraction, distribution, and use of energy in Sweden were made. Part of these were then illustrated by a diagram of flows {2}. Such a diagram is to be found on the front page on some of these reports. It describes the energy flow through Swedish society in 1971, see Fig. 3.5. The quality of the energy appears from the denotations of the different kinds of energy. Arrows turned downwards imply losses. Hydro-power is to be found in the top part of the diagram and fuel oil in the bottom part. The width of the flows are in proportion to the energy content in each respective energy form.

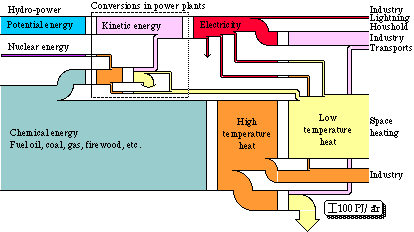
Figure 3.5. Energy conversion system in Swedish society 1971 in energy units.

Hydro-power is used to generate electrical energy. The potential energy in the power plant reservoir is transformed into kinetic energy, which is further transformed into electrical energy via a turbine and an electric generator. Nuclear energy and chemical energy are also used to produce electrical energy. This transformation takes place in condensing power plants and in combined power and heating plants. In the combined power and heat plant or cogeneration system, heat is also extracted at a low temperature through a so-called back-pressure process. Thus, all production of electrical energy takes place within the sector "Conversions in power plants". The electrical energy is then directly used, partly in industry, e.g. in electric steel furnaces and in electrolysis, partly as lighting and for electrical domestic appliances. As we see from the diagram most of the electrical energy is used within the industry to run machinery, i.e. the electrical energy is reconverted into mechanical energy. An increasingly greater part of the electrical energy is used in electric heating, partly as low temperature heat for space heating, partly as high temperature heat in industry.

The conversion of chemical energy into high temperature heat completely dominates the diagram. Oil, coal, gas, waste, and fire-wood are burnt in furnaces in order to produce heat. Most of the high temperature heat is then, via a heat exchanger, converted into low temperature heat that is used for space heating. The heating is further contributed to by district heating and electric heating. Part of the high temperature heat is used in industry, especially within the processing industry (the iron and steel works, and the pulp and paper industry). Within the iron industry, large quantities of coal are used, and within the pulp industry, large quantities of timber waste are used. The rest of the high temperature heat is used for transports. At the conversion of petrol and oil in a car engine, almost 100% of the chemical energy is converted into high temperature heat. About 20% of this heat is then further converted into mechanical energy in the car engine. Nearly half of this energy is then lost through friction in the transmission. This section is, however, not found in the diagram. The efficiency of the transports is represented through the efficiency of the car engine, and is found at the lowest conversion level in the diagram.

We see that the losses in the diagram are unimportant. Within the sector "Conversions in power plants", we find the energy losses through waste heat from nuclear plants and oil condensing power plants. There are further losses of electrical energy through conductivity losses, about 10% of the transported energy is lost in this way. On the whole about 90 TWh is lost. At a total conversion of about 460 TWh, thus about 20% of the converted energy is lost.

We also see that at each conversion process we have a one to one relation, i.e. as much energy comes in as out of the conversion process. Energy is indestructible, so all energy must remain after a conversion.

We can make a diagram of exergy flows , that illustrates the same energy system. Roughly it looks as shown in Fig. 3.6. The width of the flows here becomes proportional to the exergy content in each respective energy form. The units of the flows are, however, the same both for the energy and the exergy flow diagrams, i.e. TWh/yr. The difference now is that the width of the flows decreases radically at certain conversion processes, due to the decreasing energy quality and therefore also the decreasing exergy content. At the conversion of chemical exergy into high temperature heat, more than half of the exergy is lost. This is due to the fact that the exergy content of heat is much lower than the energy content.

Further, there are heavy exergy losses at the conversion of high-temperature heat into low-temperature heat, and also at the conversion of electricity into high or low temperature heat. As the exergy content of the high temperature heat is not utilized at the conversion of high temperature heat into low temperature heat, heavy losses are suffered here too. Consequently, a heat exchanger can not utilize the exergy loss when heat is reduced. The temperature decline in an ordinary oil furnace is thus not utilized when a flame at a temperature of about 2000^oC is used to heat water to a temperature of perhaps 80^oC. Electrical heat means that 90% of the exergy is lost at the conversion of electrical energy into low temperature heat, i.e. the electrical heat has an exergy efficiency of 10%. An efficient heat pump ("an inside-out refrigerator") should be able to improve that efficiency to at least 30%.

It appears - not unexpectedly - that the largest losses of exergy occur in domestic heating. As we can see on the right hand side of Fig. 3.6, the exergy requirements in heating are quite small, and can be decreased even quite a lot further through improvements in insulation and in taking care of the ventilation heat. To decrease exergy losses within heating even further, we can either use a good exergy converter such as the heat pump, or spread-out exergy flows such as solar heating.

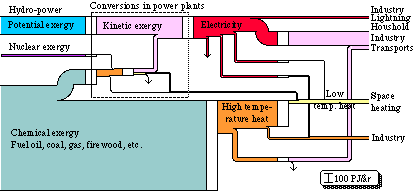
Figure 3.6. Energy conversion system in Swedish society 1971 in exergy units.

The total efficiency of the conversion process, from chemical exergy to mechanical exergy, is the same in both energy and exergy diagrams.

We can see that the losses in the exergy flow diagram are substantial. On the whole, there is a loss of about 320 TWh, i.e. 70% of the converted exergy is lost.

In the exergy diagram, inflows and outflows in exergy conversions do not need to have a one to one relationship. Exergy is not indestructible and it can be consumed.

By using diagrams such as Fig. 3.6 to describe the exergy flows in an energy system, we obtain a clearer idea of where measures should be taken to take care of the energy and exergy better.

3.5. Exergy and other resource measures

Resources are the known and retrievable parts of natural resources, i.e. those substances in ground, water and air which can be utilized. When a resource is used in society, it is often called raw material. By resource measures I mean those measures which are traditionally used to quantify these flows of resources and raw materials.

Resources are traditionally divided into energy resources and other resources. The exergy content of the energy resources is determined by multiplying the energy content with the quality index for the form of energy in question, see Table 2.1. Energy resources are measured in energy units, i.e. the same units as exergy. Other resources are usually measured in units such as weight units, volume units, or just number of units. So, within forestry we speak of m3 of timber, and in agriculture of metric tons of crops or number of animals. These measures are often chosen for purely practical or traditional reasons.

Let us call a resource used in society a commodity. Statistics on commodities are based on the quantity of each commodity. According to international norms, commodities are then divided into commodity groups, commodity subgroups, etc. The statistics are then shown in tables or diagrams in accordance with these commodity norms.

In statistics there is no common physical factor between different commodities, therefore the statistics cannot be shown in integrated form such as a flow diagram of different energy commodities, see Fig. 3.5. The only common measures used today are economic measures such as SEK (Swedish kronor). The disadvantage with such measures is that the economic value of a commodity is determined by costs for production, and supply and demand. The economic value can also be affected by subsidies and taxes on certain commodities. This means, in this case, that the value of a commodity can change even though the commodity itself has not changed in physical respect. To avoid such problems, the value of a commodity must be determined purely by the physical properties of that commodity.

It is natural to choose the exergy concept as a measure of the physical value of a commodity. Exergy is, by definition, a measure of the "physical value" of a system, in relation to its environment. In practice, the exergy content of a commodity can be calculated through multiplying the amount of the commodity by a so called quality factor, which is determined partly by the quality of the commodity, partly by the environment of the commodity. The unit for such a quality factor will then be, for example, kWh per ton, or kWh per m². The exergy content for the Swedish iron ore conversion in 1975 is calculated in Appendix B. You will find the results of this calculation in Fig. 3.9. The unit of all the flows is TWh per year, i.e. the same unit as in the energy and exergy diagrams in Figs. 3.5 and 3.6. We also see that the losses are great. Approximately 47 TWh of energy, electricity and ore is needed to produce the amount of iron and ore in question, about 7 TWh. The efficiency is thus about 15%. There will be more about this in Section 3.8, which concerns efficiency concepts.

Thus a change to quantifying flows of material by exergy only means determining the conversion factors for each material. This can constitute the first part of an expanded resource budgeting, as well as a link in an integration with the traditional energy budgeting, which I mentioned in the second part of the preceding section. One advantage with a change to measuring resources and raw materials in exergy units is that energy resources and energy raw materials will have the same units as other resources and raw materials. A division into energy resources and other resources and raw materials can often be very approximate. We can, for example, regard oil as an energy raw material and wood as another material, but the distinction is not very meaningful, since oil can also be used for production of materials just as wood can be used as fuel. Therefore, these resources ought to be considered together, in which case the concept of exergy would be a useful resource measure. This is illustrated in the diagram of the Swedish exergy conversion in Fig. 3.9.

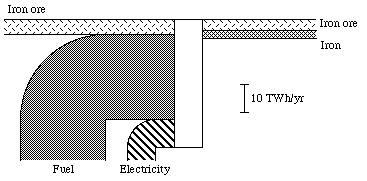
Figure 3.7. The Swedish iron ore conversion in exergy units in 1975

The concept of exergy can only show the physical quality of a commodity. The properties which are interesting in this context are then concentration, chemical composition and amount of the commodity. However, the exergy content says nothing of the physical or biological properties of a commodity, e.g. electric conductivity, nutritive value, toxicity or such properties. Commodities are only considered as carriers of exergy. However, let us assume that we are studying a specific property, for example the electric conductivity, of different materials. Then the efficiency of the exergy conversion can be a measure of the quality of the material. A material with poor electric conductivity will have greater exergy losses than a material with good electric conductivity when used as a conductor of electricity. In Chapter 4, I will discuss the efficiency of the transfer of information between different systems in terms of exergy per information unit.

3.6. Flows, deposits and funds

Energy and material resources occur partly as flows, partly as stocks. We interpret the continuously flowing solar energy and flows of water such as rivers as flows . A flow has a limited capacity, but is unlimited in time. An ecosystem, such as a forest, is a valuable stock. It is constructed out of flows of sunlight, water, carbon dioxide and minerals. This gives rise to a flow of newly formed biological matter, and a part of this can be taken out of the system without causing the destruction of the stock. Other stocks, e.g. an oil deposit, have completely different properties. These can give rise to a flow only while they are successively drained and emptied.

As to stocks, we therefore differ between dead stocks , or deposits , and live stocks , or funds . A deposit is a stock which is emptied as it is used, e.g. an oil find or a mineral ore. A fund or a live stock is a stock which, without being used up, converts one resource flow into another in a desirable manner {10}. I.e. a fund is an exergy converting system. For a hunting and gathering culture, the forest is a fund which uses small part of the incoming flow of sunlight to return flows of edible or in other ways useful plants, and animals which can be caught or hunted. For a farming culture, the cultivated land represents a similar fund, which gives a substantially greater return, but, contrary to the forest, needs to be continuously recultivated. The global system, created by the earth's atmosphere and hydrosphere, is a fund which catches and transfers solar exergy. This live stock distributes the temperature more evenly over the earth. It also distributes the water, and it has a protecting and purifying ability. Thereby it provides the basis for another fund, the biosphere, to convert the flow of sunlight into exergy rich biological matter.

Some live stocks can give a continuous return, e.g. a hydro-electric power plant. Others periodically, e.g. yearly, build up deposits which can be harvested, e.g. a field. For some funds this period of build-up can be quite long, e.g. a forest.

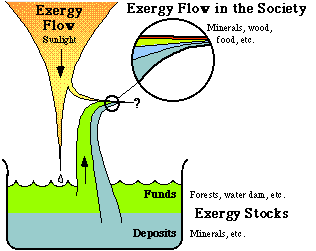
Figure 3.8. The exergy flow from the sun, and the exergy stocks on earth create the resource base for human societies on earth.

The deposits of oil and coal are added to so slowly that this is hardly of any practical interest. Peat bogs also grow very slowly, but still fast enough for the ground to be considered of interest as a fund for taking care of solar exergy. Metal ores are created by geological processes. Lake and bog iron, however, are deposited at such a rate so that the same lake can sometimes be "harvested" again in less than a century.

In Fig. 3.8, we see how the exergy flow through human society is maintained. The greater part of the exergy requirements are seen to from the terrestrial exergy stocks. Man only uses a very small part of the exergy flow from the sun, for solar heating. In society there is thus, on the whole, a continuous exergy loss. Some exergy flows, such as flows of ores, increase their exergy content when passing through society. However, other flows decrease their exergy content all the more. Let us have a closer look at the exergy conversion in the Swedish society.

3.7. Exergy conversion in Swedish society

A diagram of exergy flows can be constructed over the total conversion of energy and material which takes place in the Swedish society during one year. This will look like the diagram in Fig. 3.9.

We recognize the lower part of this diagram as the one on exergy flows in Fig. 3.6. Here we find the "inflows" of chemical exergy, nuclear exergy and hydro-electric power. Now we see the conversion of these flows in society much clearer than before.

The new flows in the diagram derive from exergy that we traditionally consider as pure materials (except solar heat) separate from the energy conversion in society. One of these is harvested forest, i.e. the amount of forest that we cut down in one year. Harvested crops are the amount of plant material produced on our cultivated land during one year. We mine ores from the ground as material. This is because the ores contain iron, a metal which is important to us. Another addition is solar heat, i.e. that part of the solar exergy which we use for domestic heating during the heating season.

We have obtained the figures for this diagram in the statistics available principally from The Central Bureau of Statistics (SCB) {39}. In addition to this, there are some approximations and evaluations since there are seldom enough figures on the quality of energy and material forms. Due to this, the inaccuracy in some flows can be up to 5 TWh/yr. This concerns in particular the flows of crops and heat.

Let us now have a closer look at the flows in Fig. 3.9. At the top we have an inflow of sunlight. This flow is estimated as 3 TWh/yr on the basis of figures on how much of domestic heating is covered by so-called passive solar heat. A south window admits about 2 kWh/m2 per day during the heating season in Stockholm. (A south window can be made to act as a small heating element by suitable control of the window shutters. {40}.) An active use of solar heat could in the future cover heating requirements completely. The main problem today is how the heat could be stored. The sun shines least when we need it the most, and vice versa. The inflow of solar heat in the Swedish exergy conversion is the only inflow which comes directly from the exergy flow of sunlight towards the earth, see Fig. 3.8. Sunlight is naturally the basis for all inflows, except for the inflow of ores and nuclear fuels. This is because all these inflows consist of solar exergy which has been stored from hundreds of millions of years as oil and coal to a few months as crops and hydro-electric power.

The topmost actual conversion in the diagram concerns the forest industry. The stock of forest, a fund, is harvested each year and the timber is used either as timber raw material or converted into paper pulp and paper. At the conversion of timber into pulp, large amounts of heat is used to boil wood chips in the processing of paper pulp. This heat is produced by burning effluence (liquors) and fuel oil. (In principle, the conversion of timber into paper pulp could be done together with an exchange of heat {41}). Approximately 70 TWh of effluence and fuel oil is converted into less than 15 TWh of heat. Together with 53 TWh of timber and 15 TWh of electricity this makes about 50 TWh of wood, pulp and small amount of paper. The efficiency of the conversion for the whole of the forest industry is then about 36%.

The next conversion process in the diagram shows agriculture and the food industry. Harvested crops are converted into food with the aid of fuels and electricity. The food consists partly of vegetable products such as vegetables and bread, partly of animal products such as milk and meat. The exergy flow of food is based on how much food swedes eat in one year (2 700 Kcal per person and day makes about 9 TWh/year). This means that the food which is thrown away is not included in the food flow, but is represented as a loss in food processing. Some estimations imply that 25 - 30% of the food that leaves the shops is thrown away. Large parts of the losses in agriculture are also inevitable since the some crops are not edible to humans, such as straw. Regrettably the use of straw in animal production has decreased conciderably the last few years. This depends to a large part on the shift in the consumption of animal products from milk and butter to pork and poultry. Due to this, the efficiency of the conversion process within food production is quite low, only about 9%. Also, the exergy content of the agricultural produce is lower than the exergy content of the inputs such as fertilizers, machine wear, and fuels {43}. About a third of the inputs of fuel and electricity in food production is used in the food processing industry.

Hydro-electric power is the next conversion process in the diagram. The losses at the conversion into electricity are relatively small. This is because the potential energy stored in the water reservoir and the electrical energy produced are both energy forms of high quality and are easy to convert into each other. There are some losses of electricity due to conductivity losses during transport. This is shown in the diagram as a narrowing of the exergy flow of electricity. I discussed the use of electricity in connection with Fig. 3.6.

Figure 3.9. Conversion of energy and matter in Swedish society in 1975 in exergy units. (Total exergy conversion 662 TWh)

In Section 3.5 and Appendix B, I made a summary of the Swedish iron ore conversion process. We see this conversion process in its context in the diagram in Fig. 3.9.

As we see in the diagram, the chemical industry converts fuels and electricity. Two thirds of the converted "fuels" can be found in the end products such as rubber, plastics and fertilizers. The chemical industry is hereby a direct example of how a traditional energy raw material such as oil can be used as a material. The "used" material can then be used as energy raw material. This is of course true about some other materials as well, such as wood and paper, though we should first of all strive to re-use material as material, not as energy raw material.

The transport sector has here been given an efficiency of conversion of about 10% , i.e. the approximate efficiency of a car, bus or truck. The transport work thus consists of exergy to overcome the air resistance and to give the vehicle an accelerative force.

The conversion of fuels into heat is divided between industrial and other premises, such as residential premises, shops premises and public premises.

Other natural exergy flows support society through more indirect means. They purify water, air and earth, and store, for example, heavy metals and sulphides. The natural ability to purify air and water could, roughly estimated, mean 0.5 TWh per year in Sweden in terms of exergy, which is too little to be represented in the diagram in Fig. 3.9. However, the same purification would, with industrial methods, cost many times more, both in terms of exergy and economically.

By using diagrams such as Fig. 3.9 to describe resource flows, we obtain a clearer idea of where to put in efforts to make better use of the resources. This should be done at all levels of the resource system.

Another advantage with the diagram in Fig. 3.9 is the division of all inflows into direct flows, flows from funds, and flows from deposits. Thus the inflow of sunlight is a direct flow of exergy from the sun. Then follow the inflows of harvested forest and crops, and hydro-power. All these flows derive from terrestrial funds of exergy. The remaining inflows of ores, nuclear fuel and fuels, come from non-renewable stocks, deposits, on earth.

To maintain a society with respect to the exergy conversion for longer periods of time, that society's exergy requirements must be almost completely covered by the solar flow and from the flows of terrestrial funds. As we can see in the diagram on the exergy conversion in the Swedish society in 1975, this is not at all the case. Thus the situation in which we find ourselves now cannot last in the long term.

3.8. Concepts of efficiency

Analogous to the two concepts energy and exergy , we can define two concepts of efficiency in an energy (and exergy) conversion process,

i) the energy in the desired end product divided by the inputs of energy. This quantity is called the "first law efficiency" in the APS-report {22}. Here it is called energy efficiency , and is denoted by .

ii) the exergy of the desired end product divided by the inputs of exergy. This quantity is called the "second law efficiency" in the APS-report {22}. Here it is called exergy efficiency , and is denoted by .

At conversions of energy between different forms, there are generally some losses of energy. Because the physical environment at energy conversions is often ignored, the energy efficiency can become greater than 1 (i.e. 100%). An example of such a conversion process is the heat pump, which can be found in Fig. 3.10. The heat pump has oceans of "free" energy (with a quality index of 0) to scoop out of its environment. We then speak of a coefficient of performance (COP) instead of efficiency. The exergy efficiency always has to be smaller than one. This is due to the fact that exergy cannot be created, it can only be destroyed or consumed.

The diagrams in Fig. 3.10 illustrate the differences between energy and exergy flows, and thereby efficiency, for 4 conversion systems: an oil furnace, electric heater, an electric heat pump and a combined power and heat plant.

At the top we see the conversion of fuel into heat in an ordinary oil furnace. The energy efficiency is limited to about 85%, principally through losses of smoke. The low value of the exergy efficiency, about 4%, is, however, due to the fact that the fall in temperature when a thousand degree flame heats water to 60 C is not utilized.

As we can see, electric heating has an energy efficiency of 100%. In the diagram for the electric heat pump we see that this is not any top limit of energy efficiency at the conversion of electricity into heat. A heat pump can, of course, also be run with fuels by connecting it to a combustion engine. The heat pump can also in this way take the place of an ordinary furnace for space heating. If the environment is ignored, the conversion of electrical energy or fuels into heat can be well over 100%. We see that in looking at exergy the picture becomes quite different. The exergy efficiency for electric heat is about 5% and for the heat pump 15%.

In Fig. 3.4, the energy and exergy flows through a condensing power plant were compared. Here we saw that the efficiency is the same from both energy and exergy point of veiw. This is because the inflow of fuels and the outflow of electricity both have a high quality, i.e. a high exergy value. In the diagram of a combined power and heat plant in Fig. 3.10, we see that the exergy efficiency is about the same for a condensing power plant as for a combined power and heat plant. We can understand this better when we see how the exergy losses are distributed in a condensing power plant. The greatest exergy loss occurred at the conversion of fuels into heat in the boiler. Since the conversion is the same in both condensing power plant and combined power and heat plant, the total exergy efficiency will be the same, about 40%. When looking at energy, circumstances are quite different. When the energy efficiency of a heat plant is stated, it is seldom shown that the theoretical maximum energy efficiency is perhaps 300%, not just 100% {4, 5}.

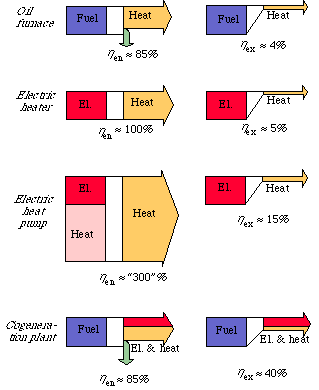
Figure 3.10. Energy and exergy efficiency for an oil furnace, an electric heater, an electric heat pump and a combined power and heat plant.

There are no general efficiency concepts today for material conversions. The natural cause for this is that there is no general resource measure. At analyses of energy in agriculture, efficiency is often given as energy input divided by energy output, i.e. energy efficiency, even though we at first see agricultural products as materials (biological matter). Within forestry, this type of efficiency concept is lacking. Efficiency concepts which are similar to exergy efficiency are used more and more in iron and steel production {45}. The measures most often used are Gibbs' or Helmholtz' free energy, see Appendix A. Together with information of the standard states of the participant substances, this gives information of the exergy efficiency of the process in question.

In Section 3.5 and in Appendix B, the conversion of Swedish iron ore was discussed very shortly. The total exergy efficiency for the iron and ore conversion was in Section 3.5 stated as 15%. For the iron conversion itself the exergy efficiency is about 6%, see Appendix B.

The concept of exergy efficiency is clearly directly related to the practical use of energy. But, according to the second law of thermodynamics, an exergy efficiency of 100% can only be accomplished at reversible processes which in principal take infinite time. A conversion process which takes place at a rate (exergy per time unit) close to zero must have a gradient other than zero.

The production of entropy and the exergy losses associated with this are discussed in Appendix D. A maximal exergy efficiency , , is defined. This depends on the rate v of the conversion process. The nature of this dependency at simple assumptions is shown in Appendix D.

It could also be useful to introduce a relative exergy efficiency , , which brings together and according to (C.7),

3.9. Exergy analysis

The exergy content in an end product does not correspond to the exergy which is used in the production. To draw up an exergy budget, it is necessary to take all different inflows of exergy in the process into account {38}. In 1974, a conference {46} was held by the International Federation of Institutes for Advanced Studies (IFIAS) at which this type of budgeting was denoted energy analysis , and Gibbs' free energy was chosen as a unit of measure. In a progress report from the project group "Energy and Society", supported by the Secretariat of Futurological Studies, there is an interesting description of energy analysis {47}.

The energy analysis has been criticized from many directions {24}. In energy analysis we often only measure one resource, energy, without taking into consideration other resources which are needed in the conversion process. This is due to the natural limits of the energy concept. By choosing exergy as a measure instead, we partly bypasse these problems. However, some general standards must be introduced. This type of budgeting should be called exergy analysis .

When we apply exergy analysis to production processes and services, we should not limit the analysis to one specific part of the process, but analyse the process as a whole as well. Exergy analysis should also be applied to various functions in society, such as transports. Exergy analysis should also be useful at an analysis of the whole metabolism of society, as described in Section 3.7. This was partly done when we analysed chains of resources.

4. Exergy and information

Exergy is a measure of how much a system deviates from its equilibrium with the environment, see Eq. (5). The more a system deviates from equilibrium the more information is needed to describe it and the greater is its capacity for carrying information {53}. There is therefore a close connection between exergy and information (or information capacity). This connection is of fundamental importance. It is discussed further in Appendix C. The relation between exergy, E in Joule (J) and information, I in binary units (bits) is

where T ₀ is the temperature of the environment measured in Kelvin (K) and where

is the fundamental constant {21}.

For example, the net flow of information capacity to the earth from the sun is about {21}, see Appendix E, Eq. (E.7),

Man only uses a fraction of this, about 5x10¹³ bits/s. Thus the relation between used and available information capacity is about 10^-24. The same relation for energy conversion is about 3x10^-5. Thus, the unused information flow from the sun is enormous. Some of the explanations for this follow below.

Information has to be stored and transported with the help of methods that are as safe as possible. To attain this, redundant codes are used, and at copying processes dissipation of extra energy is allowed, so as to render the process irreversible (one-way). The quality of the transfer increases with the loss of some of the information capacity.

At everyday communication of information, the energy consumption is quite high. This makes the exergy per bit relation high, which means that only a small part of the available information capacity is used. Therefore only a small part of the inflow of information capacity towards the earth is used as mentioned earlier, see Eq. (12). However, if we consider the conversion of solar exergy into the ordered structures of plants, we realize that even though only a small part of the primary inflow of information is captured, parts of percent, this amount is still quite enormous in itself.

It is of interest to compare the efficiency of information transfer between different systems. A measure of efficiency is the amount of exergy converted per bit of information. The dimension of this is temperature. The lower this temperature is, the more efficient is the information transfer. If this temperature is too low, however, thermal fluctuations in the environment can destroy the information, see Table 4.1.

Table 4.1. Efficiency in information transfer expressed in exergy per bit of information and in characteristic temperature

1. Data from {21}

2. Data from {48}

The sensitivity of the retina is such that the human eye functions near the quantum mechanical limit. It is in fact enough with only a few quanta to cause a reaction in the eye. Storage of information in a computer memory has a characteristic temperature of about 10⁵ times the temperature for sight. But on the other hand the time resolution, and thus the rate, is about 10⁵ times higher than for the eye. The conclusion is that living creatures and computers are each efficient in their use of exergy to receive and transfer information. The biosynthesis in a cell is after all many times more efficient.

Electronic circuits, man's ear and eye, and protein biosynthesis are drawn in a logarithmic information rate (frequency) - power diagram in Fig. 4.1. The minimum power requirements of integrated circuits has been calculated by many {49-52}. Brillouin {53} has shown that an elementary process in a circuit, such as a measurement, a storage or a logic operation, requires an energy conversion which is large in relation to kT 4x10^-21 J (at room temperature). This is necessary to avoid thermal fluctuations which are the cause of noise in electronic circuits, Brownian movement, etc. The room temperature is marked with a straight line. A process must ordinarily be far above this line to avoid serious disruption from thermal fluctuations. The protein biosynthesis {54} is surprisingly close to this critical line. The transfer from messenger RNA to proteins, which uses half of the power requirements, is actually below this line. This is possible because all of 4.3 bits of information are transferred at each transformation. The ear and the eye occupy strikingly large areas in the diagram, covering many orders of magnitude. Electronics is probably the best technology we know today, from an exergy efficient viewpoint. But, as Fig. 4.1 shows, life itself is far more efficient in its use of exergy to construct biological matter.

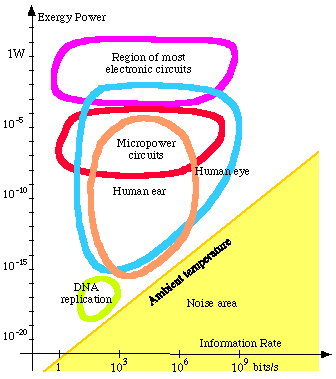
Figure 4.1. Information rate - power diagram of information transfer

Biological structures live by transforming energy from one form to another. The solar exergy is used to build up complicated organic matter. This information is transferred from generation to generation. The information which is stored in the genetic matter (DNA molecule) directs the construction of matter. When biological material, e.g. wood or cellulose, is used as construction material, it is these structures and this information that we benefit from.

Both exergy and information are measures of the deviation from a reference environment . The exergy is the maximal amount of work that can be derived from such a deviation, but the work is also needed to maintain and transfer information. The relationship between exergy and information is therefore a very close one.

5. Concluding remarks

All living systems are part of a flow of energy and matter. They receive energy and matter at a low entropy and emit it at a high entropy. Thereby a net inflow of negentropy or exergy is maintained, which keeps the system alive. In living organisms exergy is used to drive metabolic processes and to maintain and develop structures from molecular level and upwards. It is therefore important to understand how exergy is converted. The exergy concept should thus be useful to the geophysical and biological sciences, as well as the technological sciences.

The metabolic processes in society are usually described within economics, but also within other sociological sciences. Even these processes are driven by exergy. It would therefore be natural to relate sociological and economical analyses of a society on an analysis of the exergy conversion in this society.

Exergy is only a physical concept which can be used to describe the reality in which we live. Unclear definitions of concepts and measures can slow down or obstruct a rational tackling of important resource problems. The measure of energy has different meanings in different situations, not least depending on where or by whom it is done. The exergy concept does not provide a solution of the energy and resource problems. The exergy concept is a useful tool in describing the energy and material conversion in society. From technological sources it is often said that the exergy concept is a useless measure since it depends on the environment. In my view, this is on the contrary the value of the exergy concept. The human society must live in harmony with nature, human activity must be adapted to the environment. All utilization of resources and disposal of waste products affect nature. This effect is strongly related to the amount of exergy in the utilized resource or the disposed waste.

Appendix A Derivation of the exergy concept

Consider a system A in a surrounding system A ₀, assumed to be homogeneous and to be large in comparison to A , fig. A.1. The "environment" A ₀ can be characterized by its intensive parameters T ₀, p 0 and (temperature, pressure, and chemical potentials). The corresponding parameters for A are T , p and i . (For the moment A is also assumed to be homogeneous.) The extensive parameters for A are U , V , S and n_i ([internal] energy, volume, entropy, and the number of moles of different chemical elements). The extensive parameters for A ₀ are accordingly U ₀, V ₀, S ₀ and n_{i 0} and are assumed to be large in comparison to the corresponding quantities for A ,

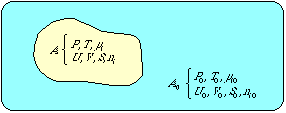
Figure A.1. A system A in an environment A 0.

The combined system A+A₀ is assumed to be isolated (no exchange of matter or energy with the surroundings) apart from work W extracted from A ,

Interaction between A and A ₀ can take place in a controlled way through the interface of A . Since A is small, Eq. (A.1), this does not change the intensive parameters of A ₀,

The entropy differential of the environment A ₀ is

where we have used (A.2). The total entropy differential system and environment is

This may be written as

where we have introduced the exergy E ,

If we use the relation

in (A.7) we get

which shows that E vanishes at equilibrium (T =T ₀, p =p ₀, i = i ₀ ).

Assume now that A evolves towards equilibrium with its environment A ₀ without doing any work (dW = 0). The exergy is then changed from E to 0 and the total entropy is changed from to , (eq stands for equilibrium). By integrating (A.6) we then get

and thus

Now defining negentropy as

we then have

The exergy of A thus is T ₀ multiplied by the negentropy for A and its environment A ₀. We note that in the definition of exergy (A.7) only the intensive parameters of A 0 appear.

During the process through which equilibrium is attained the exergy thus changes by -E (from E to 0). Let the total entropy increase be and let the total work extracted be W . Then the integrated version of (A.6) is

or

Since

with equality only for a reversible process =0, we have

i.e. the exergy E is the maximum amount of work that may be extracted from A in its process of reaching equilibrium with its environment, A ₀.

We may subtract from (A.7) the corresponding equation at equilibrium. Since E vanishes at equilibrium we then find

which is a useful equation for practical determinations of exergy.

In special cases exergy differences are related to differences of other, better known, thermodynamic potentials, as described in Table A.1.

Table A.1. Relations between differences in exergy and in other thermodynamic potentials.

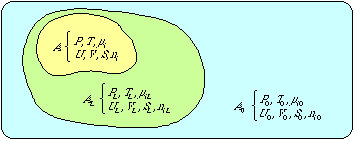
Figure A.2. System A in a local environment A_L in an environment A ₀.

It may be of interest to consider the case of a system A in a local environment A_L which in its turn is included in a global environment A ₀ (Fig. A.2). We may then define a "local" exergy .

which is related to the "global" exergy

through

where E_{L 0} gives the contribution of exergy due to the deviation of the local environment from the global one,

which is the exergy expression (A.9) for A with the intensive parameters of A_L replacing those of A . However E_{L 0} is not an exergy function. For instance it is clearly not positive definite.

The exergy or negentropy may be said to be a measure of the contrast of a system against an average "gray" background, see Eqs. (A.9) and (A.12). It is therefore natural that these concepts are closely tied to information theory, see Appendix C.

Appendix B Exergy content of materials

Assume that the temperature T and the pressure p are constant i.e. T =T ₀ and p =p ₀, then according to Eq. (A.9) we have

From chemistry we have that the chemical potential for an element i may be written as

where ai is the activity for the element i and is the chemical potential for the element relative to its reference state .

Further we have

where ci is the concentration of the element i . From (B.2) and (B.3) we may write (B.1) as

The exergy of a material may thus be calculated from its chemical potential and from its concentration in its actual state and in its reference state. This is illustrated in an example from the Swedish iron production in 1975. This illustration is to be regarded as a simple example of the use of the exergy concept within resource accounting.

If we only consider one element we may instead write Eq. (B.4) as

The Swedish mining industry is totally dominated by iron ore. The Swedish iron ore has an average iron content of about 60% (weight percentage) and it usually consists of magnetite in which the iron ore has the chemical composition Fe₃O₄. We then have c =60%.

Now suppose that the bed-rock represents a standard environment and that its iron atoms are in their (energetically) lowest ionization state, i.e. Fe²⁺-ions, then we have c ₀=5% and the difference in chemical potential becomes 50 kJ/mole {56}.

With T ₀ =15^oC, the exergy content of magnetite iron ore with 60% iron becomes 56 kJ/mole ore 170 kWh/ton.

In an analogous way we find that the exergy content of pure iron becomes 92 kJ/mole or 460 kWh/ton.

The Swedish production of iron ore was in 1975 approximately 36 Mtons. (Estimated on the basis the production in 1974.) If we assume all this ore to be magnetite iron ore, since most of the Swedish iron ore is, then the ore represents a total exergy quantity of 6.1 TWh.

The production of iron was in 1975 roughly 6 Mtons, representing an approximate quantity of 2.7 TWh. To produce this iron about 10 Mtons of ore was needed, corresponding to 1.7 TWh together with 10 TWh of electrical exergy and 30 TWh of coal, coke and other fuels. The exergy efficiency in the iron production process then becomes =6%. Figure 3.7 illustrates the situation.

Appendix C Efficiency concepts at conversions of exergy

A conversion process taking place at a non-zero rate v (exergy per unit of time) must be driven by a non-zero gradient g . For many applications it is probably sufficient to assume linearity , as in Eq. (E.2),

where is a constant independent of g .

The entropy production per unit of time connected with such a conversion process is quadratic with respect to v (compare Eq. (E.4))

where does not depend on v . If several ways are possible for the conversion process to occur from the initial to the final form of energy then let ₀ assign the lowest possible value of for the conversion process being studied. Then we have a minimum entropy production per unit time

and hence a minimum exergy destruction per unit time where T ₀ is the environmental temperature. Thus, the maximum amount that can go into desired outputs (exergy per unit time) is

we are thus led to define

iii) the maximal exergy efficiency related to the conversion rate v as

where

is the characteristic power connected to the conversion process.

iv) We can also connect (ii) and (iii) and define a relative exergy efficiency for a non-zero rate conversion process

Appendix D Exergy and information

Thermodynamics deals with the physical laws of systems containing many particles. From a macroscopic point of view the systems are small (approximately 10^-21 m³), but from a microscopic point of view they are large ( 10^-21 m³ contains approximately 10⁹ atoms). Thus, it is impossible to have a detailed knowledge of the motion of individual particles. In statistical mechanics , which provides the theoretical basis for the understanding of thermodynamics, we take advantage of the large number of particles and use statistical methods to describe macroscopic properties as average properties resulting from the motion and interaction of many particles.

Information theory deals with a system of incomplete information (Shannon). The general problem of how to take into account, in an unambiguous way, the available (incomplete) information was successfully tackled by Jaynes. As Jaynes showed, statistical mechanics is a special instance of information theory. Conversely, powerful concepts and methods developed in statistical mechanics may be extended to other fields through information theory.

Let the system being described consist of N particles. The number of possible states depends exponentially on N . Let the probability for the j th state be realized by P_j ,

The entropy is then defined in statistical mechanics as,

where k is Boltzmann's constant.

The probabilities at equilibrium are those that maximize entropy S under whatever constraints on the system that may be given

The (excess) negentropy of the system described by the probabilities P_j then is

The information content is, according to information theory (Yourgrau), in binary units (bits)

As an example, if the system contains N different particles with 2 possible states each, then = 2^N . If there are no constraints, all are equal 2^-N . Complete information about the system (one P_j equal to unity, the others vanishing) then gives I = N. For each particle there is then information equivalent to one yes or one no answer to a specific question. Each such answer amounts to one binary unit (bit) of information. From Eqs. D.4 and D.5 we see that negentropy and information are very simply related

where

plays the rule of fundamental constant. Thus one bit is equivalent to 1.0x10^-23 J/K of negentropy.

The relation in Eq. A.10 between exergy and entropy,

("tot" stands for the total system, which is here only called the system) combined with Eq. D.6 gives us the following relation between exergy and information

Thus k'T₀ = 2.9x 10^-21 J is the amount of exergy connected to one bit of information at room temperature.

It should be noted that "information " is a measure not necessarily of actual meaningful information but rather of information capacity . It can also be thought of as a measure of order or structure .

Appendix E Exergy and some idealized thermodynamical systems

1. Equilibrium

An isolated system A at equilibrium has maximum entropy, S = S _eq. Let the system be described by the intensive variables X_i(x,t) depending on position x within A , and time t . The values of the variables X_i are determined through the condition of maximum S ,

The entropy may decrease only temporarily through fluctuations, as indicated in Fig. E.1.

At equilibrium, parameters such as temperature and entropy are well-defined.

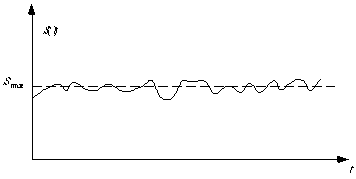
Figure E.1. Entropy as function of time for a system in equilibrium

2. A system not deviating too far from equilibrium

Consider a small volume around the point x of the system A , see Fig. E.2. If V is macroscopically small but still large enough to contain a large number of particles it may be considered at a specific time to constitute a system which has reached equilibrium in . (The relaxation time for reaching internal equilibrium in is assumed to be small compared to a typical period of time describing interaction with the surroundings.) Thus, temperature, pressure, entropy density and so on may be defined as functions of the point x and time t .

Figure E.2. A small volume V surrounding the point x in a system A

Flows J_i (x ,t ) are driven by gradients of the intensive variables X_i . A linear relationship can be assumed

where the coefficients L_ij satisfy the Onsager relations

When the system evolves the entropy increases. Let the entropy production per unit volume and time be

. Then {59}

where

We see from Eqs. (E.4) and (E.5) that for systems which are not isolated, , there is an entropy production whenever there is a gradient. The entropy production has its minimal value for a source-free gradient,

III. Systems far from equilibrium. Living systems.

A system may be maintained away from equilibrium if it lies in an energy flow and receives energy from one system and passes it to away to another. For such a system A , see Fig. E.3, the inflow of energy (temperature T ₁) carries low entropy and the outflow (temperature T ₂<T ₁) carries high entropy. If the power is P and the average temperature of A is T ₀ (T ₁>T ₂>T ₀), then the net exergy gain per unit time , W is

This exergy flow can be used to construct and maintain structures far away from equilibrium.

Figure E.3. A system A of average temperature T ₀ in an energy flow P .

For living organisms equilibrium means death. Human beings, as well as animals in general, stay away from equilibrium (i.e. stay alive) by extracting chemical energy in the processing of food into waste. This energy is then passed on to the environment as heat. The whole biosphere lives by converting high frequency (heat) radiation emitted to space, see Fig. 3.3. The fundamental process here is the photosynthesis in the plant. Physically, of course, living systems are extremely complicated. A much simpler example of Fig. E.3 is a metal rod conducting heat from a hot reservoir to a cold reservoir.

If the deviation from equilibrium is not too great, a system in a position between a steady energy giver and a steady energy receiver evolves into a stationary state . This is for instance true for the metal rod in the example just mentioned.

A stationary state not far from equilibrium is characterized by minimal entropy production,

and the boundary conditions imposed by the energy giver and the energy receiver. Thus, in the evolution towards a stationary state, the entropy production decreases steadily until it reaches the minimum value determined by Eq. (E.8).

If a system is in a negentropy (or exergy) flow , Ref. {26} and if self catalytic processes are possible, then fluctuations may be used as starting points for producing structure and order out of a more chaotic state, Refs. {34} and {35}. This is the way life once began on earth, Ref. {34}. The description of such phenomena, however, is outside the scope of this report.

A simple way of helping a system which involves self catalytic processes is to enclose it within a shell of some sort. A living cell is an obvious example of this.

IV. The exergy of an ideal monoatomic gas

Figure E.4. A gas in a container in an environment of the same gas.

Consider an ideal monoatomic gas enclosed in a container in an environment of the same gas, see Fig. E.4. If T or p deviate from T ₀ or p ₀, work may be extracted from A. To determine the exergy we use Eq. (A.16). Assuming that the gas is thin enough to be considered as an ideal gas, we have for the volume V , energy U , and entropy S of A

where n is the total number of moles, and

We vary volume and temperature and keep n constant, n = n _eq, we then get

Expressed in terms of relative deviations from equilibrium

the exergy is

where g (x ) is the function, also see Fig. E.5

We see that g (x ) increases rapidly with increasing negative value of x . For the temperature part in Eq. (E.13) this means that if the gas is much colder than the environment it carries a large amount of exergy.

The divergence at x = 1 is connected to the use of Stirling's formula (E:15) in the derivation of Eqs. (E.9). For a large n we have

When Stirling's formula is no longer valid since n becomes small (see the comment of this in Chapter 2 in Ref. {22}), the gas is no longer to be regarded as an ideal gas.

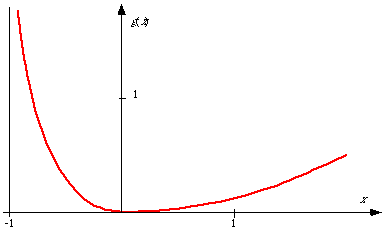
Figure E.5. The function g (x ) = x ln(1+x ).

References

1. B. Eriksson, K.-E. Eriksson, K. Olsson, and G. Wall, "Towards an integrated accounting of energy and other natural resources", Report no. 75-33, Inst. of Theoretical Physics, Chalmers University of Göteborg and University of Göteborg, Göteborg 1976.

2. Governmental report no. SOU 1974:72-76, "Energy Research" ("Energiforskning", in Swedish).

3. Governmental proposal no. 1975:30, "Energy Conservation etc." ("Energihushållning m m", in Swedish).
4. Governmental report no. SOU 1975:60, 61, "Energy Preparedness in Time of Crisis", ("Energiberedskap för kristid", in Swedish).

5. "The combined power and heat plant in Västerås", ("Kraftvärmeverket i Västerås"), prospectus from the Power Company of the Community of Västerås (Västerås Stads Kraftvärmeverk AB) and Aros Power Company (AB Aroskraft) 1974, (in Swedish).

6. "Combined power and heat plant. What is that?" ("Mottryckskraft. Vad är det?"), prospectus from Stal-Laval, Finspång, 1975, (in Swedish).

7. F. Cottrell, Energy and society. The relation between energy, social changes and economic development , Mc Graw-Hill Book, New York, 1955.

8. R. G Wilkinson, Poverty and progress , Methuen, London, 1973.

9. K. Boulding, "The Economics of the Coming Spaceship Earth", in Enviromental Quality in a Growing Economy , Henry Jarret, ed., Baltimore, John Hopkins Press, pp. 3-14.

10. N. Georgescu-Roegen, The Entropy Law and the Economic Process , Cambridge, Mass: Harvard Univ. Press, 1971. Southern Economic Journal , Chapel Hill, N.C. vol. 41, 1975.

11. G. Adler-Karlsson, Textbook for the 80's (Lärobok för 80-talet ), Lund, 1975, (in Swedish).

12. G. Borgström, see for instance Focal Points - A Global Food Strategy , Macmillan, New York, 1973.

13. H.T. Odum, Enviroment, Power and Society , Wiley, New York, 1971.

14. H.T. Odum and E.C. Odum, Energy Basis for Man and Nature , New York, Wiley, 1976.

15. Reports from the group Energy and Society at the Secretariat of Futurological Studies (Energi och Samhälle , in Swedish):

T. B. Johansson, M. Lönnroth, "Energy analysis - an introduction" ("Energianalys - en introduktion"), report no. 403,

T. B. Johansson, M. Lönnroth, and P. Steen, "Energy and Freedom of Action" ("Energi och handlingsfrihet"), report no. 409.

Reports from the group Resources and Raw Materials at the Secretariat of Futurological Studies (Resurser och Råvaror , in Swedish):

"Resources and Raw Materials - a Starting Point for a Futurological Study" ("Resurser och råvaror - några utgångspunkter för en framtidsstudie"), report no. 301,

C. A. Olsson, "About Natural Resources and Economics" ("Något om naturresurser och ekonomi"), report no. 302,

"Renewable Resources" ("Förnyelsebara råvaror"), report no. 304.

16. "The Material Conversion Process in the Society" ("Materialomsättningen i samhället"), report no. 182 from The Academy of Engineering Science (IVA), 1974, (in Swedish).

17. "Natural resource cycles" ("Kretslopp"), Yearbook from the Swedish Natural Science Research Council (NFR) 1976/77, Lund, Liber, 1976 (in Swedish).

18. Z. Rant, Forschung Ing.-Wesens , vol. 22, 36, 1956.

19. H. D. Baehr, Energie und Exergie , VDI-Verlag, Düsseldorf, 1965.

20. R. B. Evans, A Proof that Essergy is the only Consistent Measure of Potential Work , Thesis, Dartmouth College, Hanover, New Hampshire, 1969.

21. M. Tribus and E. C. McIrvine, Scientific American , vol. 224, no. 3, p. 179, 1971.

22. Efficient Use of Energy, a Physics Perspektive , American Physical Society (APS), January 1975.

23. N. B. Ericsson, "The Use of Energy and The Social Evolution - an Analysis of Substitution Conditions" ("Energianvänding och samhällsutveckling - analys av substitions- förhållanden"), report no. 75-08-2, Inst. of Heat and Power Technology, University of Technology in Lund (in Swedish).

24. "Analysis of Energy Inputs in Production" ("Analys av energiinsatser i produktion och funktion"), report no. 92 from The Academy of Engineering Science (IVA), Stockholm, 1977 (in Swedish).

25. T. Simmons, Teknisk Tidskrift , vol. 107, no. 7, 1977 (in Swedish).

26. E. Schrödinger, What is life? , Cambridge University Press, 1944.

27. S. Carnot, Reflections on the Motive Power of Heat , 1824, American Society of Mechanical Engineers, 1943.

28. J. W. Gibbs, "A Method of Geometrical Representation of the thermodynamic properties of substances by means of surface", 1873, The Collected Works , Yale University Press, vol. 1, 1928.

29. G. Darrieus, Engineering , vol. 130, pp. 283-285, 1930.

30. J. H. Keenan, Mechanical Engineering , vol. 54, p. 199, 1932.

31. J. H. Keenan, Thermodynamics , Wiley, New York, 1941.

32. G. Gustafsson, J. Lyttkens, and S. G. Nilsson, "The energy forms of the universe, the energy flow to the earth, energy - not only a question of technology" ("Universums energiformer, energiflödet till jorden, energi- inte endast en fråga om teknik"), report from the Centre for Interdisciplinary Studies of Human Condistions (Centrum för tvärvetenskapliga studier av människans villkor), University of Göteborg, Göteborg, 1974 (in Swedish).

33. M. K. Hubbert, Scientific American , vol. 224 , no. 3, p. 60, 1971.

34. P. Glansdorff and I. Prigogine, Thermodynamics Theory of Structure, Stability and Fluctuations , Wiley-Interscience, New York, 1971. A short estimation is presented in "Thermodynamics of Evolution", I. Prigogine, N. Nicolis, A. Babloyante, Physics Today , pp. 23-28 and pp. 38-44, 1972.

35. M. Eigen, Die Naturwissenschaften , vol. 58, p. 465, 1971.

36. H. T. Odum, Ambio , vol. 2, p. 220 (1973) see also the classical work: A. J. Lotka, Proc. Nat. Ac. Sci. , vol. 8, p. 147, 1922.

37. J. Szargut, T. Styrylska, Brennstoff-Värme-Kraft , vol. 16, p. 589, 1964.

38. S. Berry, Bulletin of the Atomic Scientists , vol. 9, p. 8, 1972.

39. Statistical Abstract of Sweden 1976 , the Central Bureau of Statistics (SCB), Sweden, Liber, 1976.

40. F. Hagman, VVS , vol. 48, no. 3, p. 69, 1977, (in Swedish).

41. S. Nilsson, Ambio , vol. 3, no. 6, p. 222, 1974.

42. Governmental report no. Df Jo 1975:2, "Production target and preparadness in food supply" ("Produktionsmål och livsmedelsberedskap" in Swedish).

43. "Resource flows in Swedish agriculture and forestry 1956 and 1972 with regard to energy flows (Resursflöden i svenskt jord- och skogsbruk 1956 och 1972 med tonvikt på energiströmmar), report no. 64 from the Inst. of Economics and Statistics, University of Agriculture, Uppsala, 1975 (in Swedish).

44. M. W. Gilliland, Science , vol. 189, p. 1051, 1975.

45. S. Eketorp, Kemisk Tidskrift , no. 6, p. 54, 1976 (in Swedish).

46. IFIAS (International Federation of Institutes of Advanced Study), Workshop reports, "Energy Analysis", report no. 6, 1974 and "Energy Analysis and Economics", report no. 9, 1975. For a short summary see: L. Kristoferson and S. Nilsson, Ambio , vol. 5, p. 27, 1976.

47. T. B. Johansson and M. Lönnroth, "Energy analysis - an introduction" ("Energianalys - en introduktion"), Stockholm, 1976 (in Swedish).

48. A. L. Lehninger, Biochemistry , Worth Publishers, N.Y., 1970.

49. J. T. Wallmark, Inst. Phys. Conf. Ser. No 25 , pp. 133-167, 1975.

50. R. W. Keyes, Proc. IEEE , vol. 63, p. 764, 1975.

51. C. H. Bennett, IBM J. Res. Development , vol. 17, p. 525, 1973.

52. R. Landauer, IBM J. Res. Development , vol. 5, p. 183, 1961.

53. L. Brillouin, Science and Information Theory , 2nd ed., Academic Press, New York, 1962.

54. J. D. Watson, Molecular Biology of the Gene , 2nd ed., W.A. Benjamin Inc., New York, 1970.

55. R. Reif, Fundamentals of Statistical and Thermal Physics , pp. 291-296, McGraw-Hill, 1965.

56. CRC, Handbook of Chemistry and Physics , vol. 49, p. D-42.

57. C. E. Shannon and W Weaver, The mathematical theory of communication , University of Illinois Press, 1963 (1st ed. 1949).

58. E. Jaynes, "Information theory and statistical mechanics", lectures at Brandies Summer Institute in Theoretical Physics, 1962.

59. W. Yourgrau, A. van der Merwe, and G. Raw, Treatise on Irreversible and Statistical Thermophysics , Chapter 1 and 2, McMillan, 1966.

Go to (in English)

| Main page | Menu | Home | Who'sWho? | Curriculum vitae |
| Ph.D. Thesis | Bibliography on Exergy >2000 publ. |
| Exergy, Ecology and Democracy | Scientific papers | Courses |
| Documents to download in PDF format | Why? What? Can? |

Gå till (på svenska)

| Huvudsida | Meny | Vem? | Artiklar etc. |
| Exergi, Ekologi och Demokrati | Exergilära |
| Kurser | Videoband | Vetenskaplig och pedagogisk verksamhet |